Adaptable Data Consolidation
Data integration that is machine verifiable, captures data lineage, preserves data relationships through transformations, and scales complexity with quadratically lower costs.
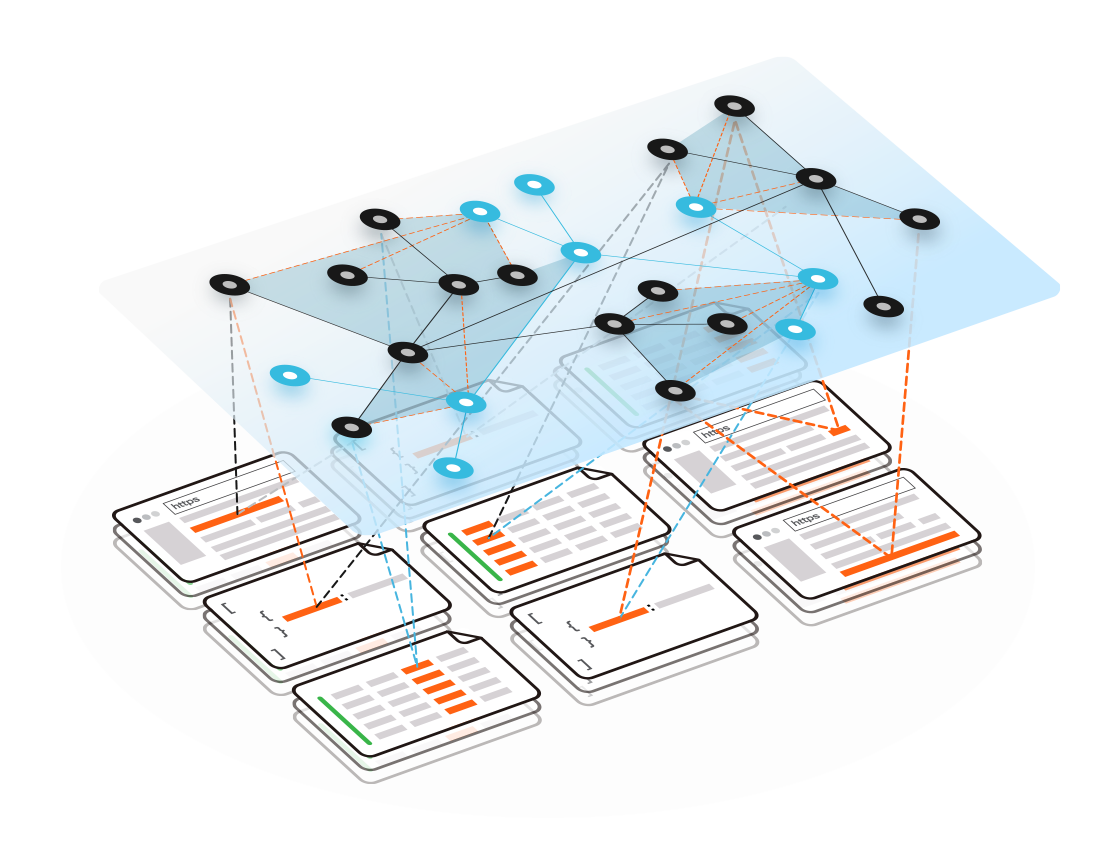
Adaptable Data Consolidation
Data integration that is machine verifiable, captures data lineage, preserves data relationships through transformations, and scales complexity with quadratically lower costs.
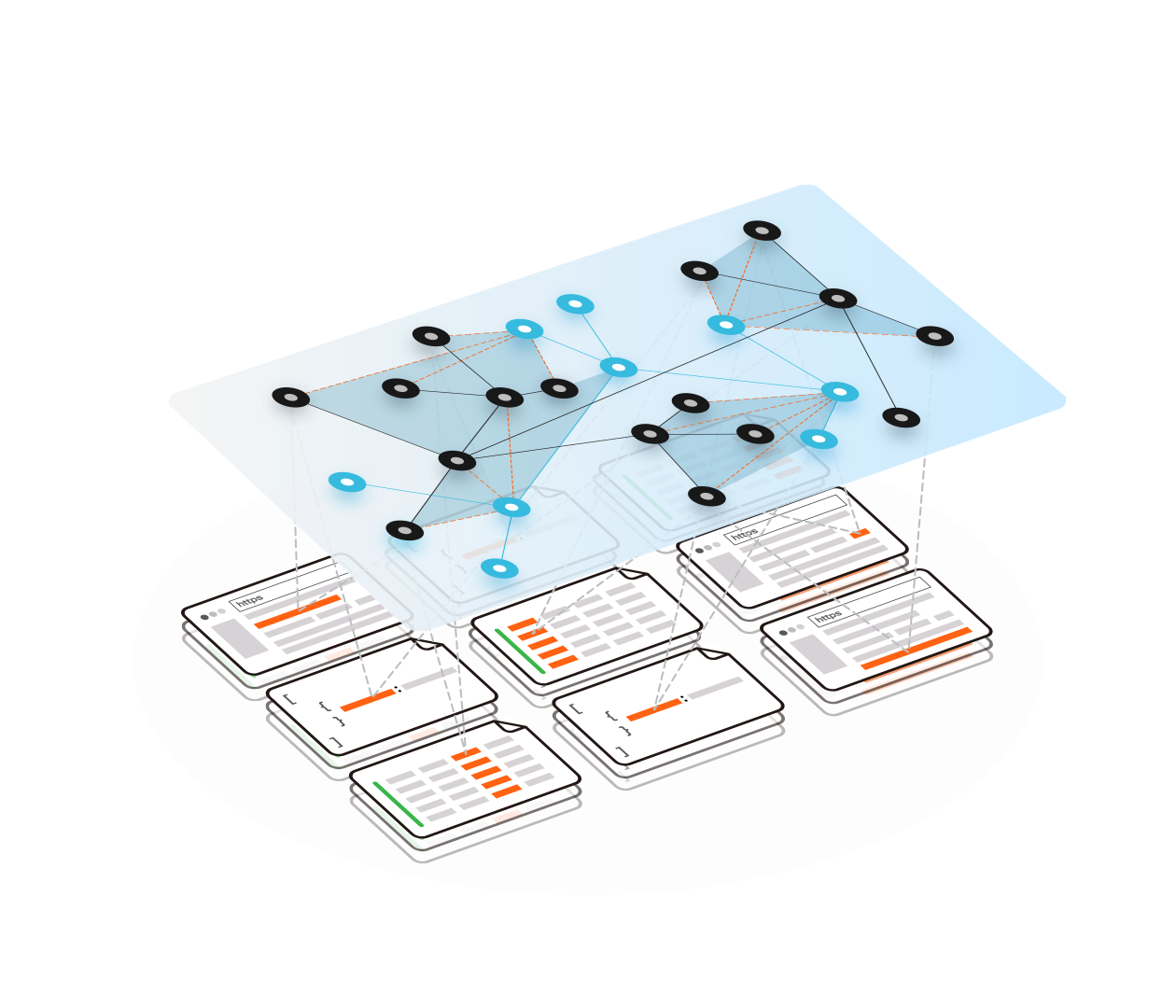









Tame Big Complexity
Consolidating hundreds of complex enterprise data sources doesn’t have to be overwhelming.
Learn how Conexus makes the most intimidating data unification efforts practical.

Joshua Shinavier
Uber
Current solutions for enterprise data modeling are often informal and ad hoc. Conexus’ use of [math] as an interlingua for data can dramatically increase productivity by removing barriers to data integration.
Murray Cooper
Honeywell Aerospace
We strongly endorse Conexus. They have changed the landscape with their technology platform which fits very nicely into our design and engineering processes.
Experts in Algebraic Data Integration
This new approach maximizes integration adaptability, transparency and reliability and scales complexity with diminishing costs instead of exploding costs. Conexus is the leader in Algebraic Data Integration enabled by Categorical Algebra.
Uber Data Consolidation
How Conexus helped Uber consolidate hundreds of thousands of data sources stored in over a dozen different technologies.

Supercharge Your Data Architects
Conexus helps architects build universal data models bottom-up by mapping sources to each other. With composable and machine-verifiable mappings, the perfect data model is discovered, not designed.
Smash Data Bottlenecks
Unleash the value of all your data, faster. The future of your company depends on it.
Resources - Company - News - Contact - Privacy Policy
@2023 Conexus AI, Inc. All Rights Reserved.
